応答曲面法の注意点と多目的設計探査＜2017年11月28日＞

実験計画法の手法である応答曲面法は、
 
  ①応答曲面用実験の計画
  ②応答曲面関数の導出

  ③応答曲面関数を利用した最適解探索

 
という手法の体系です。①では、中心複合計画やD最適計画など、よく知られる直交表とは異なる計画が使用されます。②では、2次項・交互作用項を生成して説明変数とした上で、重回帰分析を使って応答曲面関数を導出します。最近ではガウス関数の重畳として曲面を表現するノンパラメトリック^※な方法も見られます。③では、網掛け法，ダウンヒル・シンプレックス法， 遺伝的アルゴリズムなどの探索法が使用されます。
 
（注）ノンパラメトリックとは、1次項・2次項の係数という意味を持ったパラメータを使用しないことを指しています。代表的な方法にRBF（Radial Basis Function）があります。
 
皆さんは重回帰分析を行ったとき、偏回帰係数や標準偏回帰係数を見て、各因子の効き方を考察すると思います。応答曲面法においても同様に、応答曲面関数の各係数の大きさを見て、固有技術的に想定される応答の変化に概ね一致しているかどうかを考察することが重要です（パラメトリックな方法だからこそ可能なのです）。
 
ここで注意しなければならないのが、統計ソフトによって求められる係数が異なるということです。以前、筆者が日本科学技術研修所主催のシンポジウムで話したところ、「ソフトによって応答関数が異なるのは本当なのか？」と2ちゃんねるで話題になりました。このことからも、一般にはあまり知られていないことが窺えますが、知っていないと考察時に悩むことになります。
 
代表的なものは、2次項の係数の符号です。この符号が正のとき、応答曲面が上凸か下凸か、どちらになっているでしょうか。実はStatWorksはこの符号が正のときは応答曲面は下凸なのです。この原因は、－1，0，1と並んだ1次項を2乗するときに、1，0，1とするか、－1，0，－1とするかにあります。他の多くの海外製ソフトは逆です。『２次項が正なら上凸』の方が直観的に受け入れやすいからです。
 
次に注意しなければならない点は、各因子の寄与の大きさを重回帰分析にならって標準偏回帰係数で比較してはならないということです。一般に、重回帰分析においては、説明変数・目的変数を（0，1^2）に基準化したときの偏回帰係数、すなわち標準偏回帰係数を見て各因子の寄与の大きさを比較します。各説明変数が取り得る範囲の中で動くとき目的変数がとれだけ変化するか＝傾きの大きさを、横軸の分散を同じにして見ていることになります。
 
しかし、実験の計画空間は離散的で、D最適計画などは繰り返しも不揃いになりますので、分散を同じにしても、各説明変数の動く範囲が同じになる訳ではありません。本来は基準となるコード化された実験空間に写像して、そこから求められる係数で比較すべきなのです。
 
まだ問題があります。2次項や交互作用項は統計ソフト内で1次項から生成されています。例えば、2次項は1次項を中心化してから2乗して求めます。2因子の回転可能かつ直交する中心複合計画においては1次項の水準が（－1.414，－1，0，1，1.414）ですので、2次項は（2，1，0，1，2）となります。これらの水準値を出現回数を考慮してコード化すると1次項は（－0.5，－0.354，0，0.354，0.5）、2次項は（0.53，0.177，-0.18，0.177，0.53）になります。ここで注意しなければならないのは、果たして横軸の幅は同じになっているのかという点です。基準となる計画空間のキュービック部分の変化幅は1次項が－0.354～0.354で0.707であるのに対して2次項では-0.18～0.177で0.354と小さくなっています。その結果、コード化してもなお2次項の係数は1次項より2倍大きく観測されます。
 
この対応として、海外製のソフト（STATISTICAなど）では基準化を行わず、1次項のキュービック部分が（－1，0，1）のとき、2次項は（2/3，－4/3，2/3）（下凸）と変数変換して、変化幅をいずれも2としています。すなわち計画空間のキュービック部分の大きさを揃えているのです。これによって、係数の大きさから寄与の大きさを類推することが可能になります。このソフトの日本語版では、これを「重心／測定多項式」と言っていますが、たぶん、centering（中心化）を重心、scaling（尺度化）を測定と誤訳したのではないかと筆者は考えています（拙著では尺度化は基準化と勘違いされるので項目化としました）。多目的最適化においては、yも変化幅を揃えておけば、重みの違いをy間について反映できるため、０から１の値を持つ満足度という指標に置き換えています。
 
一部のテキストでは、執筆者に応答曲面法の実務経験が無いからか、従来の重回帰分析にならって標準偏回帰係数を見るように書いていますが、それは1次項間でのみ可能です。標準偏回帰係数で1次が強いのか2次が強いのかを判定するのは間違いです。残念ながらStatWorksには項目化の機能がありませんので、このような判定は困難です。
 
計画空間の変換には、中心化、さらには再中心化・項目化などの変換があります。ソフトが表示する偏回帰係数はそれによって異なります。しかし、変換ルールに沿って変換した説明変数を代入すればどれも予測値（点推定値）は同じになりますので、ご安心ください。
 
以上、応答曲面法の注意点を述べて来ました。最後に、応答曲面法を超える新手法である多目的設計探査について、最適解を探索するケースを例にご紹介したいと思います。
 
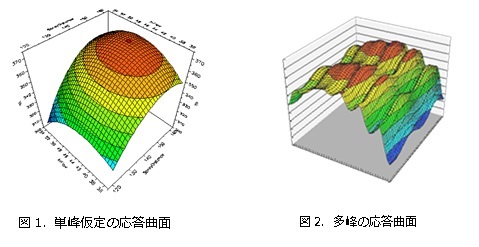
設計パラメータの上下限値で規定される設計空間の中から最適解を探索する場合、一般に応答曲面法を用いますが、その場合は図１のような単峰仮定で最適解を探索します。しかし現実的には、図２のごとくバンピーな応答も存在します。このような多峰の応答の最適化は、データサイエンスの一手法である多目的設計探査を用いることにより可能になります。
 
まず、空間内に満遍なく実験点を布置します。空間充填計画という方法を用います。そしてその観測値をノンパラメトリック回帰によって関数化します。RBFやクリギング（Kriging）といった関数化の方法を使い、多峰の特性を再現します。最後に遺伝的アルゴリズムを用いて、一気に多数の成立解を見つけ出します。
 
従来は、設計空間内には唯一解しかないという前提（単峰仮定）でしたが、実際には、車でも家電でも多種多様な設計がなされ、ほぼ互角の性能で競っています。つまり、設計空間は多峰なのです。その成立解を特許で全て押さえられてしまうといった危機が迫っています。
 
是非、古典論の最終兵器「応答曲面法」を超える新兵器「多目的設計探査」を学んで、戦っていきたいものです。

 

 

 
 

この多目的設計探査は、一般社団法人『HPCI（ハイパフォーマンス・コンピューティング・インフラ）コンソーシアム』でも活用が議論されると共に、国産初のジェット旅客機MRJ（ミツビシ・リージョナル・ジェット）や、2020年打ち上げ予定の新型ロケット「H3」に搭載するLE-9エンジンのターボポンプ設計に活用されています。
 
紙幅の都合で大まかなご紹介となりましたが、日本科学技術連盟で開催される「モノづくりにおける問題解決のためのデータサイエンス設計コース」でこの多目的設計探査が扱われる予定です。ご興味のある方には、当コースの受講をお勧めいたします。

• モノづくりにおける機械学習セミナーベーシックコース
• モノづくりにおける機械学習セミナー入門コース
• 技術力で差をつけるための実験計画法実践セミナーエキスパートコース
• 多変量解析法セミナー入門コース
• 品質管理セミナー入門コース【QC検定2級レベル対応】