Mail News Archives

SQC

計数値データの解析＜2018年02月26日＞

計数値データの解析

　今回は計数値データの解析について簡単に振り返りたいと思います。

■計数値データの性質

　データには計数値データと計量値データがあります。計量値データは、長さ・重さなど連続的な値をとるものであり、一方で、計数値データは不良率やキズの数など離散的な値をとります。率や個数で表現される計数値データは計量値と比べて比較的サンプリングが容易で、改善の目標設定によく用いられます。
　一般に、不良率のデータは二項分布に、キズの数のデータはポアソン分布に従うことが知られています。これらの分布から直接確率を求め厳密に解析することも可能ですが、近似が妥当かどうかは計数値データの解析の多くの場合は正規近似もしくはカイ二乗近似に基づく方法を用います。ただし、サンプルサイズが十分大きいことが近似条件です。不良個数ないしはキズの数が5個以上観測できるようにサンプルサイズを設定することが一つの目安となります。

■計数値データの解析

　ある製品Ａの母不良率が10％と高く、改良を加え製品Ａの試作品を400個作ったところ、不良品は32個であった。このとき母不良率は減少したといえるのかを知りたい時に適用される検定方法が母不良率に関する検定です。二項分布に従うことから母数であるサンプル数nを400個、母不良率Pを10％とした二項分布のもと、不良が32個以下となる確率を求め、有意水準の5%と比べ、高いかどうか判定する厳密な解析方法もありますが、計算手順自体が面倒や、煩雑になります。そこで、正規分布近似法に基づく方法を用います。二項分布の正規近似として、直接近似、ロジット変換や逆正弦変換がございます。特に、0や１に近傍しているところの近似では、直接近似よりは、ロジット変換や逆正弦変換の方が近似の精度が高いということも頭に置きながらどの近似法がいいか選択しましょう。ここでは、最も一番簡単な直接近似について紹介致します。
　直接近似とは文字通り単純に二項分布の母平均、母分散をそのまま用います。つまり、母不良率 Pは母平均 p，母分散 P(1-P)/nの正規分布に従うとし、検定統計量を計算します。検定手順は、計量値の場合の検定方法と同様で、帰無仮説と対立仮説を考え、あらかじめ有意水準を定め、棄却域を求めます。次に、帰無仮説が成り立つ仮定のもと検定統計量を計算し、有意かどうか棄却域と照らし合わせ判定します。
　それでは今回のケースを例に検定してみましょう。帰無仮説は改良後の製品Ａの母不良率と改良前の母不良率が同じで10％であるのに対し検出対立仮説は改良後の母不良率の方が改良前の母不良率と比べて減少しているということが対立仮説となます。この場合、母不良率が減少したかどうかを検出したいので、片側検定を用います。有意水準を5%と定めると、棄却域は
－1.645以下となります。正規分布の片側5%の1.645という値と両側5%の1.96という値は覚えておくと非常に便利です。次に、検定統計量の計算です。直接近似による正規近似を用いるので検定統計量は

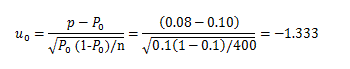
となります。－1.333は－1.645より大きいので有意と判定されない。従って今回のケースの母不良率は減少したとはいえないという結果になります。今回のケースでは、サンプル数400では少なく、10%－8% = 2%の差を検出できなかった可能性があります。不良率のデータはサンプルが容易な一方で、データは良品か不良品の二値の情報のみですので、情報量が少ないという点に注意する必要があります。情報量が少ない分、小さい差を検出するには大きなサンプルサイズが必要となります。
　ただ、母不良率の検定の統計手法としては先の通りですが、統計的品質管理としては計数値データの背後には計量値的な特性があるということを常に意識して品質管理活動を進めることの方が重要です。
　不良率やキズの数などは結果系としての特性値であり、工程不良の要因解析を行うための情報としては乏しく、実際にはキズの長さや深さなどの計量値の情報が工程改善には必要になります。結果系としての不良率の少ない差を検出するためにサンプルサイズを計算して、統計的仮説検定を実施するのではなく、キズの長さや深さなどの原因系を特性値として取り扱えば、計量値のアプローチが適用できます。
　もちろん、特性値の性質や測定機器によっては、計数値データしかとることができずそのデータに基づいて解析を進めなければならない場合や、結果系ではなく原因系として計数値を取り扱わなければならない場合もあります。その場合にはこの計数値データの解析を適用してください。計数値データの解析は他に母欠点数に関する検定・推定や分割表による検定、ある特定の分布に従っているかを検定する適合度検定や、母不良率に関する分散分析や回帰分析など、様々な場面に適用できる手法がありますので、興味があればぜひもう一度学習してみて下さい。